Aplicando la Ley de Biot-Savart que relaciona la inducción magnética, B(t), con la causa que la produce, es decir, la corriente i(t) que circula por la bobina, se obtiene que el flujo magnético Φ(t) que abarca es igual a:
.png)

se le denomina Coeficiente de autoinducción L, el cuál, como se puede ver, únicamente depende de la geometría de la bobina. Se mide en Henrios. Así pues obtenemos la expresión
.png)
Pero además, al ser el flujo magnético variable en el tiempo, genera, según la Ley de Faraday, una fuerza electromotriz (f.e.m.) de autoinducción que, según la Ley de Lenz, tiende a oponerse a la causa que la produce, es decir, a la corriente eléctrica que genera dicho flujo magnético. Por esta razón suele llamarse fuerza contraelectromotriz. Ésta tiene el valor:

Ley de Lenz
"Cuando varía el flujo magnético que atraviesa una bobina, esta reacciona de tal manera que se opone a la causa que produjo la variación"
Es decir, si el flujo aumenta, la bobina lo disminuirá; si disminuye lo aumentará. Para conseguir estos efectos, tendrá que generar corrientes que, a su vez, creen flujo que se oponga a la variación. Se dice que en la bobina ha aparecido una corriente inducida, y, por lo tanto, una fuerza electromotriz inducida.
Ley De Faraday
La Ley de Lenz solamente habla de la forma en que se comporta la bobina pero no dice nada acerca de la magnitud de la corriente o de la fuerza electromotriz inducida. Faraday llegó a la conclusión que la fuerza electromotriz E vale:

Siendo:
E: f.e.m. inducida
n: número de espiras de la bobina
Df: Variación del flujo
Dt: Tiempo en que se produce la variación de flujo
El signo menos (-) indica que se opone a la causa que lo produjo (Ley de Lenz)
En conclusión, la ley de Lenz explica como se comporta la bobina en presencia de campos o corrientes variables, mientras que la ley de Faraday determina la relación entre magnitudes
Suponiendo una bobina ideal sin pérdidas de carga, aplicando la segunda Ley de Kirchhoff, se tiene que:


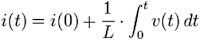
No hay comentarios:
Publicar un comentario